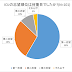
決定木とは
さて、この本で決定木を勉強します。
尾崎 隆
技術評論社
売り上げランキング: 141,877
技術評論社
売り上げランキング: 141,877
- 決定木とは、できるだけ外れているものをよけるように条件分岐して順番を決めていくアルゴリズム
- 説明変数はカテゴリ型でも数値型でもどちらでも大丈夫。
タイタニック号の生存率
- タイタニック号の生存率をRを使って可視化する
- 生存をYES、死亡をNOとする
- 決定木を使うと、こんなことがわかるらしい
- すでにタイタニック号の生存率を分析している人がいらっしゃったので参考になりそう。(ここでは割愛する)
- 「女性と子供は優先させろ!」という船長の命令だったらしいので、「できるだけ外れているものをよけるように条件分岐して」という意味で、左側に性別と年齢の変数があるのは決定木の特徴をよく出しているなと思う
どのキャンペーンページが効果的だったか分析する
ただし、
と出てきてしまった。どうやら、mvpartのサポートが終わってしまったようなので、代替案としてrpartを使う。
参考)http://www.ric.co.jp/book/contents/pdfs/953_mvpart.pdf
Warning in install.packages :package ‘mvpart’ is not available (for R version 3.1.2)
> require(rpart) > d1 <- read.csv("C:/workspace/R/DM_sampledata/ch6_4_2.txt", sep="") > View(d1) > d1$cv<=as.character(d1$cv)#CVカラムをcharacter(文字列型)に直す [1] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE [13] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE [25] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE [37] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE [49] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE [61] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE [73] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE [85] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE [97] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE [109] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE [121] TRUE TRUE TRUE TRUE TRUE > d1[d1$cv=="1",7] <- "YES"#cvが1の時、yes > d1[d1$cv=="0",7] <- "NO"#cvが0の時、no > head(d1) d21 d22 d23 d24 d25 d26 cv 1 1 0 1 1 0 1 YES 2 0 1 0 1 1 0 NO 3 1 0 1 0 1 1 YES 4 0 1 0 0 1 0 NO 5 1 0 0 1 1 1 YES 6 1 0 0 1 0 1 YES
> d1.rp <- rpart(cv~.,d1) > d1.rp n= 125 #サンプルサイズは125 node), split, n, loss, yval, (yprob) * denotes terminal node # 結果出力の凡例 # node:ノード( ステップ)、split: 分岐 条件 # n: その分岐で扱っ たサンプル の個数、loss: 誤っ て分類された個数 # yval: 分類結果( 学習ラベルのどちらに分類されたか) # yprob: 最終 的 な 分類 確率 # *は 終端 ノード 1) root 125 62 NO (0.5040000 0.4960000) 2) d21< 0.5 58 5 NO (0.9137931 0.0862069) * 3) d21>=0.5 67 10 YES (0.1492537 0.8507463) 6) d22>=0.5 7 3 NO (0.5714286 0.4285714) * 7) d22< 0.5 60 6 YES (0.1000000 0.9000000) *
見づらいので、樹形図にする。
> install.packages("rpart.plot") > library(rpart.plot) > rpart.plot(d1.rp, extra = 4,uniform=T)
そうすると、こんな感じの図が出てくる。
- d21を見ていない(d21 < 0.5)場合、9%の顧客が購入する(91%は購入しない)
- d21を見ていて(d21 >= 0.5) 、かつ
- d22を見ていない(d22 < 0.5)場合、43%の顧客が購入する(57%は購入しない)
- d22を見ている(d22 >= 0.5)場合、90%の顧客が購入している(10%は購入していない)
- 今度は決定木の分析結果を最適化、枝を剪定(pruning)する必要がある
- 今では枝が多すぎず、ノイズが大きいので、パラメータの剪定が必要
- pltcp関数を利用して、汎化能力(Generalization Ability)を上げる
「plotcp関数は、分類性能の評価法のひとつである「交差検証法(Cross Validation:CV)」を用いて、決定機のえだの 数を変化させながら、決定機の気を茂らせるためのパラメータのひとつである「複雑性パラメータ(Complexity Parameter : CP)」の値とCV誤差(xerror:図中x-val Relative Errorと表示されている値)との関係をプロットするものです。」
- 一般に枝の数を決める基準として、xerrorの最小値からその標準偏差ひとつ分の範囲内で最大のxerror値(Min + 1SE)を選び、それに対応する枝の数を採用するものとされている。
> plotcp(d1.rp)
Size of Treeが2で、cp(複雑性パラメータ) = 0.11、、xerrorの最小値が0.2
この値をもとに、rpart関数に値を追加する
> d1.rp2 <- rpart(cv~.,d1, cp=0.11) > plot(d1.rp2,uniform=T,margin=0.2) Error in plot.new() : figure margins too large
Error in plot.new() : figure margins too large
と出てきてしまって、用は図形をPlotする際の余幅が足りないらしいので、dev.new()で別窓を開いて、再度実行したらうまくいった。
> dev.new() > d1.rp2 <- rpart(cv~.,d1,cp=0.11) > plot(d1.rp2,uniform=T,margin=0.2) > text(d1.rp2,uniform=T,use.n=T,all=F)
- このように、汎化能力を上げることによって、精度は高くなる
- 一方で、なるべく細かいビジネス要素をみて、何が重要か知りたい場合、あえて剪定しない。
どのようなカテゴリの商品やキャンペーンがリピーター増につながるのかを分析する
- 次は目的変数が2値データ、説明変数が二値データ、連続データを含んだものを利用して決定木計算を行う
- ch7_3_2.txtを利用して、分析を行う
- あるECサイトにおける個人の顧客300人分の購買データと、キャンペンページへのアクセスデータがミックスされたものとなる。
- v1:書籍(円)
- v2:酒類(円)
- v3:ゲームソフト(円)
- c1:キャンペーン1(1=実施、0=未実施)
- c2:キャンペーン2(1=実施、0=未実施)
- c3:キャンペーン3(1=実施、0=未実施)
- retention:翌月リピート(Yes, No)
- データをインポートして、見てみる
> head(d2) v1 v2 v3 c1 c2 c3 retention 1 1900 5900 3800 0 0 1 No 2 2900 0 6600 1 0 0 Yes 3 2600 0 4100 1 0 1 Yes 4 3200 0 5100 1 0 0 Yes 5 2200 0 5600 0 0 1 No 6 5100 0 4200 1 0 1 Yes
- このような、二値データと、連続変数を含んだものでも、決定木計算を行うことができる
- 参考書通りやってみる。
> d2.rp <- rpart(retention~.,d2) > plot(d2.rp,uniform=T,margin=2) > text(d2.rp,uniform=T,n=T,all=F,cex=2)
- なんか違う....
- 少しコードをかえてやってみる
> rpart.plot(d2.rp,uniform=T)
ほむほむ。うまくいった。
- キャンペーン1にアクセスし(C1 >= 0.5)で、かつ書籍で2400円以上を支払った場合(V1 >= 2400)が一番リピート率が高い(38%)
- キャンペーン1をアクセスせず(C1 < 0.5)、さらに酒類の購入額が2850円未満で(V2 < 2850)で、書籍購入金額が2550円以上(v1>= 2550)の場合はリピート率が高い(8%)
- キャンペーン1にアクセスせず、かつ酒類に2850円以上支払いを行っている人が、最もリピート率が低い
ということがわかる。
尾崎 隆
技術評論社
売り上げランキング: 141,877
技術評論社
売り上げランキング: 141,877